动态规划法
经常会遇到复杂问题不能简单地分解成几个子问题,而会分解出一系列的子问题。简单地采用把大问题分解成子问题,并综合子问题的解导出大问题的解的方法,问题求解耗时会按问题规模呈幂级数增加。
为了节约重复求相同子问题的时间,引入一个数组,不管它们是否对最终解有用,把所有子问题的解存于该数组中,这就是动态规划法所采用的基本方法。
动态规划的一个重要性质特点就是解决“子问题重叠”的场景,可以有效的避免重复计算
问题: 求两字符序列的最长公共字符子序列
问题描述:字符序列的子序列是指从给定字符序列中随意地(不一定连续)去掉若干个字符(可能一个也不去掉)后所形成的字符序列。令给定的字符序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一个严格递增下标序列<i0,i1,…,ik-1>,使得对所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一个子序列。
解决方案:
-
枚举法
这种方法是最简单,也是最容易想到的,当然时间复杂度也是龟速的,我们可以分析一下,刚才也说过了cnblogs的子序列
个数有27个 ,延伸一下:一个长度为N的字符串,其子序列有2N个,每个子序列要在第二个长度为N的字符串中去匹配,匹配一次
需要O(N)的时间,总共也就是O(N*2N),可以看出,时间复杂度为指数级,恐怖的令人窒息。
-
动态规划
考虑最长公共子序列问题如何分解成子问题,设
A=“a0,a1,…,a<sub>m-1</sub>”,
B=“b0,b1,…,b<sub>m-1</sub>”,
并 Z=“z0,z1,…,z<sub>k-1</sub>” 为它们的最长公共子序列。
不难证明有以下性质:
(1) 如果a<sub>m-1</sub>=b<sub>n-1</sub>,则z<sub>k-1</sub>=a<sub>m-1</sub>=b<sub>n-1</sub>,且“z0,z1,…,z<sub>k-2</sub>”是“a0,a1,…,a<sub>m-2</sub>”和“b0,b1,…,b<sub>n-2</sub>”的一个最长公共子序列;
(2) 如果a<sub>m-1</sub>!=b<sub>n-1</sub>,则若z<sub>k-1</sub>!=a<sub>m-1</sub>,蕴涵“z0,z1,…,z<sub>k-1</sub>”是“a0,a1,…,a<sub>m-2</sub>”和“b0,b1,…,b<sub>n-1</sub>”的一个最长公共子序列;
(3) 如果a<sub>m-1</sub>!=b<sub>n-1</sub>,则若z<sub>k-1</sub>!=b<sub>n-1</sub>,蕴涵“z0,z1,…,z<sub>k-1</sub>”是“a0,a1,…,a<sub>m-1</sub>”和“b0,b1,…,b<sub>n-2</sub>”的一个最长公共子序列。
这样,在找A和B的公共子序列时,如有 a<sub>m-1</sub>=b<sub>n-1</sub>,则进一步解决一个子问题,找“a0,a1,…,a<sub>m-2</sub>”和“b0,b1,…,b<sub>m-2</sub>”的一个最长公共子序列; 如果a<sub>m-1</sub>!=b<sub>n-1</sub>,则要解决两个子问题,找出“a0,a1,…,a<sub>m-2</sub>”和“b0,b1,…,b<sub>n-1</sub>”的一个最长公共子序列和找出“a0,a1,…,a<sub>m-1</sub>”和“b0,b1,…,b<sub>n-2</sub>”的一个最长公共子序列,再取两者中较长者作为A和B的最长公共子序列。
既然是经典的题目肯定是有优化空间的,并且解题方式是有固定流程的,这里我们采用的是矩阵实现,也就是二维数组。
第一步:先计算最长公共子序列的长度。
第二步:根据长度,然后通过回溯求出最长公共子序列。
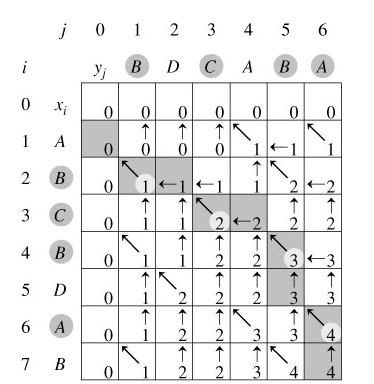
现有两个序列X={x1,x2,x3,...xi},Y={y1,y2,y3,....,yi},
设一个C[i,j]: 保存Xi与Yj的LCS的长度。

根据上面的公式其实可以发现C[i,j]一直保存着当前(Xi,Yi)的最大子序列长度。
回溯输出最长公共子序列过程:
长度的问题我们已经解决了,这次要解决输出最长子序列的问题,
我们采用一个标记Flag[i,j],当
①:C[i,j]=C[i-1,j-1]+1 时 标记Flag[i,j]= 0, "left_up"; (左上方箭头)
②:C[i-1,j]>=C[i,j-1] 时 标记Flag[i,j]=1, "up"; (上箭头)
③: C[i-1,j]<C[i,j-1] 时 标记Flag[i,j]= -1,"left"; (左箭头)
算法分析:
由于每次调用至少向上或向左(或向上向左同时)移动一步,故最多调用(m + n)次就会遇到i = 0或j = 0的情况,此时开始返回。返回时与递归调用时方向相反,步数相同,故算法时间复杂度为Θ(m + n)。
代码
这里的 b[][] 充当了 前文中 Flag[][]的角色
#include#include #define MAXLEN 100void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN]){ int i, j; for(i = 0; i <= m; i++) c[i][0] = 0; for(j = 1; j <= n; j++) c[0][j] = 0; for(i = 1; i<= m; i++) { for(j = 1; j <= n; j++) { if(x[i-1] == y[j-1]) { c[i][j] = c[i-1][j-1] + 1; b[i][j] = 0; } else if(c[i-1][j] >= c[i][j-1]) { c[i][j] = c[i-1][j]; b[i][j] = 1; } else { c[i][j] = c[i][j-1]; b[i][j] = -1; } } }}void PrintLCS(int b[][MAXLEN], char *x, int i, int j){ if(i == 0 || j == 0) return; if(b[i][j] == 0) { PrintLCS(b, x, i-1, j-1); printf("%c ", x[i-1]); } else if(b[i][j] == 1) PrintLCS(b, x, i-1, j); else PrintLCS(b, x, i, j-1);}int main(int argc, char **argv){ char x[MAXLEN] = {"ABCBDAB"}; char y[MAXLEN] = {"BDCABA"}; int b[MAXLEN][MAXLEN]; int c[MAXLEN][MAXLEN]; int m, n; m = strlen(x); n = strlen(y); LCSLength(x, y, m, n, c, b); PrintLCS(b, x, m, n); return 0;}
参考